| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 투포인터
- 파이썬
- 머신러닝
- 프로그래머스
- 재귀
- Virtual Memory
- 완전탐색
- 정렬
- 코테
- 1일1솔
- Python
- OS
- 재귀함수
- sort
- 신나는함수실행
- two pointer
- 브루트포스
- Algorithm
- ML
- dfs
- Loss
- 알고리즘
- CS
- 코딩테스트
- BF
- python3
- backtracking
- Github
- 백준
- 백트래킹
- Today
- Total
이것저것 공부 기록하기
[MachineLearning] Simple Linear Regression(단순 선형 회귀) 본문
Linear Regression이란?
Linear Regression은 OLS(Ordinary Least Square, 최소제곱법)이라고도 불리는 가장 오래된 회귀용 선형 알고리즘이다. Linear Regression의 Hypothesis는 다음과 같다. 기본적인 가정은 ${x}$와 ${Y}$가 선형관계라는 것이다.

Linear Regrssion(선형 회귀)은 회귀분석(입력 변수 ${x}$의 정보를 활용하여 출력 변수 ${Y}$를 예측하는 방법)의 기본적인 방법이며, 이러한 선형회귀를 바탕으로 좀 더 복잡한 비선형회귀가 개발되기도 했다.
변수가 2개 이상이면 다중선형회귀라고 한다. 우선 여기서는 변수가 하나인 단순선형회귀부터 살펴보자.
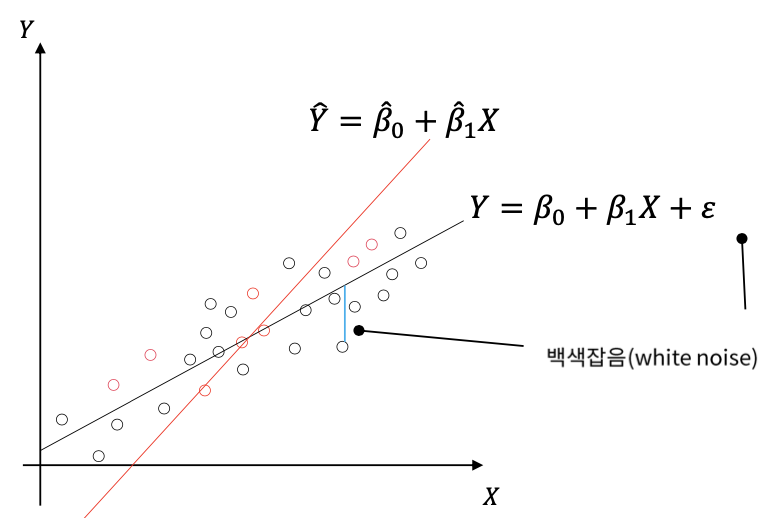
- 단순선형회귀의 식은 다음과 같이 나타낼 수 있다. $${Y} = \beta_{0} + \beta_{0}{X} + \varepsilon$$
- 또한, 입력 변수가 ${X}$, 출력 변수가 ${Y}$일 때, 단순선형회귀의 식은 오른쪽 그림의 검은 선처럼 나타낼 수 있다.
- $\beta_{0}$는 절편(intercept), $\beta_{1}$은 기울기(slope)이며 합쳐서 회귀계수(coefficients)로도 불린다.
- 검은 점: 모집단의 모든 데이터
- 빨간 점: 학습집합의 데이터
- 실제 $\beta_{0}$과 $\beta_{1}$은 구할 수 없는 계수로 데이터(학습집합)를 통해 이 둘을 추정해서 사용한다.
그림에서 우리가 알고 싶은 것은 검은색 선이고 추정해야 하는 것은 빨간색 선이다. 그렇다면 어떻게 이걸 추정해야 할까?

일단, 실제 값과 추정한 값의 차이가 적으면 적을수록 좋다.
실제값과 추정값의 차이를 잔차(residual)라고 하며 이를 최소화하는 방향으로 추정해야 한다.
잔차는 왼쪽 그림과 같이 나타낼 수 있다. 이러한 잔차의 제곱합(SSE)를 최소화하는 방향으로 구한다.
왜 다른 것도 아닌 잔차의 제곱합을 최소화시키는 걸까?
잔차의 합이 0이 되는 해는 무수히 많기 때문에 유일한 해를 찾지 못하기 때문이다.
또한, 잔차의 절대값의 합은 미분이 불가능한 형태로 나타난다.
하지만, 잔차의 제곱합은 미분이 가능한 형태로 유일한 해를 찾을 수 있게 된다.
$$SSE = \sum_{i=1}^{n}e{_{i}^{2}} = e{_{1}^{2}} + e{_{2}^{2}} + ... + e{_{n}^{2}}$$
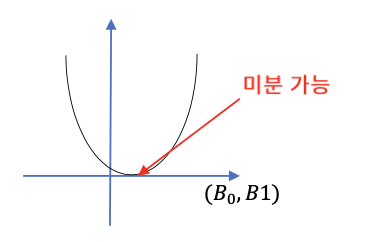
SSE가 최소가 되는 지점은 기울기가 0이 되는 지점이며, 선형회귀는 이러한 잔차의 제곱합(SSE: Error sum of squares)를 최소화하는 방법으로 회귀 계수를 추정해내는 것이다.
다음 포스트에서는 회귀계수의 추정과 모델 정확도 평가의 대표적인 지표인 ${R}^2$에 대해 다뤄보겠습니다.
'MachineLearning' 카테고리의 다른 글
| [MachineLearning] Stratified K-Fold (0) | 2021.10.20 |
|---|---|
| [NLP 논문리뷰] GPT3 - Language Models are Few-Shot Learners (0) | 2021.05.26 |
| [MachineLearning] Loss Function vs Cost Function vs Objective Function (0) | 2021.03.30 |
| [MachineLearning] Loss Function(손실 함수) 이해하기 (0) | 2020.07.10 |
| [MachineLearning] 앙상블 소개 / XGBoost 와 LightGBM 비교 (0) | 2020.07.03 |




